Understanding Slant Range in Radar Systems

What is Slant Range?

Radars measure the distance to targets based on the direct line-of-sight path from the sensor to the target.  This distance is known as the slant range. When targets are at a different elevation than the radar, the slant range will differ from the ground range, which is the projection of that distance onto the Earth's surface.

The radar beam can have a large vertical extent, meaning that targets may be detected at substantial heights above or below the radar.  If there is significant difference in height between the target and the radar, the slant range may differ appreciably from the ground range.  

 

 

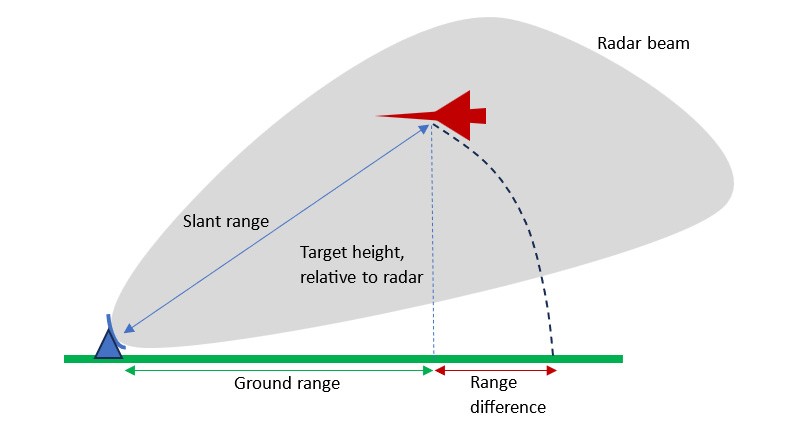
The divergence between the slant range and ground range is a function of the height separation between the radar and the target, defined by simple trigonometry:  

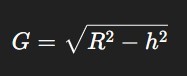
Ground Range =√(Slant Range² - Height Separation²)
 
Equivalently:

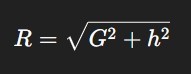
Slant Range =√(Ground Range² + Height Separation²)

The greatest deviation between slant range and ground range occurs at short ranges or steep elevation angles, where the relative height becomes a larger proportion of total range.  At the extreme, where the target is directly above or below the radar, the ground range would be zero but the slant range would be the height difference.  However, it should be remembered that the radar’s antenna pattern may well preclude targets being visible at such steep elevation angles anyway.   

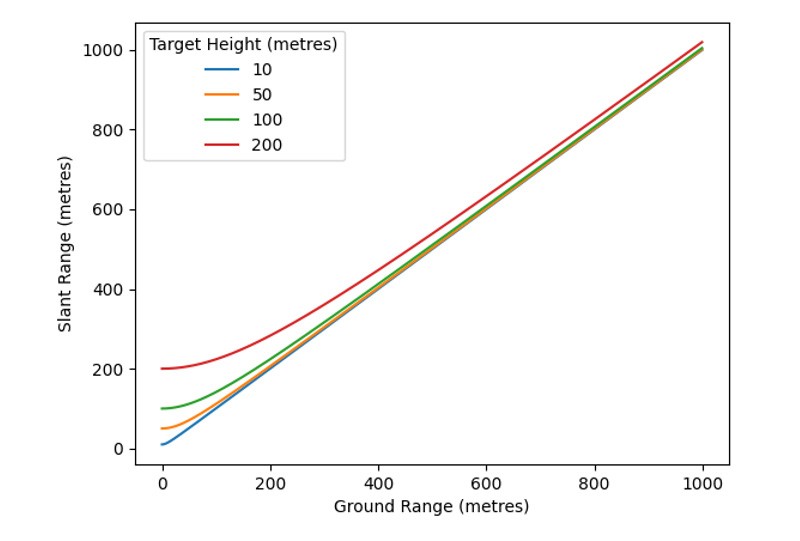
Figure 2 below shows slant range compared to the ground range for targets at different heights, relative to the radar.  As the target range increases, both values converge asymptotically.  This convergence is quicker for smaller heights.    

 

 

An alternative depiction, as represented in figure 3 below, shows the difference in slant range and ground range, as a function of ground range, for different relative target heights.  These curves effectively represent the elevation angle as a function of range, normalized to the target’s height.

 

 

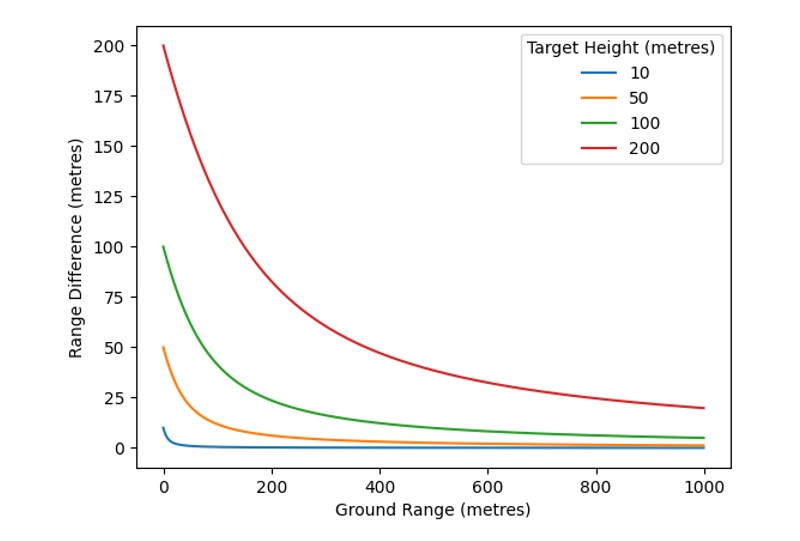
Slant range may become significant in situations where the radar is mounted at height, looking for surface targets (e.g. coastal surveillance and airport surface movement) or where a surface radar is looking for targets at significant altitude (e.g. air surveillance).  As can be seen in the graphs above, the difference in range varies with the height of targets relative to the radar.  Since a 2D radar inherently has no height information (a target is merely known to be somewhere within the beam, at the slant range) it is therefore not possible to correct for every possible target height.  However, in scenarios where targets of interest are at a fixed height relative to the radar, such as an airport surface movement radar looking for ground traffic, this height difference is fixed.        

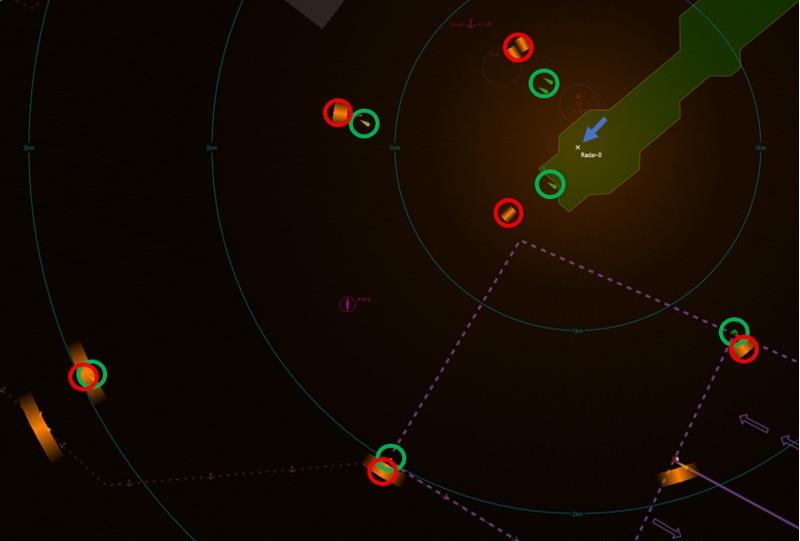
The consequence of the difference in slant range and ground range is that targets derived from the radar data will appear at increasingly wrong ranges as they approach the radar and will not align with GPS-based targets (e.g. AIS, ADS-B) or physical features on a map.  This can be seen in figure 4 below where the radar is marked by the blue arrow, physical targets (in this case buoys) are circled in green and the corresponding radar returns are circled in red.

 

 

To summarise, the key consequences of the difference in slant range and ground range are:

•  Radar returns misaligned with GPS overlays.
•  False positioning on maps or fusion displays.
•  Increasing error near the radar.